This beginner level TouchDesigner tutorial explores a method for looping noise for the purpose of creating looping animations. In it we will recreate a Processing sketch by Étienne Jacob, which is featured in his blog post Drawing from noise, and then making animated loopy GIFs from there. The article has lots of great examples of working with noise, and was how I first encountered the looping technique myself. Below is a quick breakdown of the specific looping noise technique that is covered in the tutorial. There are a few other ways of deriving loops from noise which I will cover in subsequent tutorials in this mini-series.
If you have questions, comments, suggestions or corrections please leave them below, and thanks for watching and reading!
Note: If you’re exporting a movie file or GIF, there’s one step I missed mentioning in the last section of the video. After stopping at the end of the timeline pause playback and click ‘+’ to move to the first frame. Then press record followed by play to start playback. This will prevent doubling the last frame in your loop.
TouchDesigner Build: 2019.14650 or later. Download an example .toe file here.
Topic Timestamps:
00:00 - Intro
02:01 - Building the Render Network
03:50 - Instancing a Grid
05:29 - Displacement with Pattern CHOP and Noise TOP
09:38 - Shaping Noise Amplitude
11:30 - Cropping to a Circle
12:50 - Feedback Motion Blur
15:30 - Looping Noise (Concept)
18:15 - Looping Noise (Application)
22:32 - Exporting as a GIF
The Looping Noise Technique
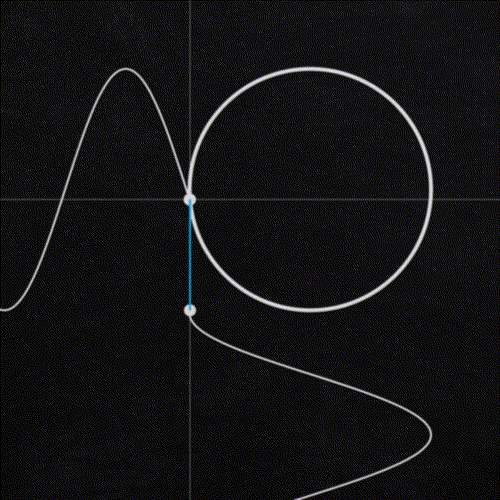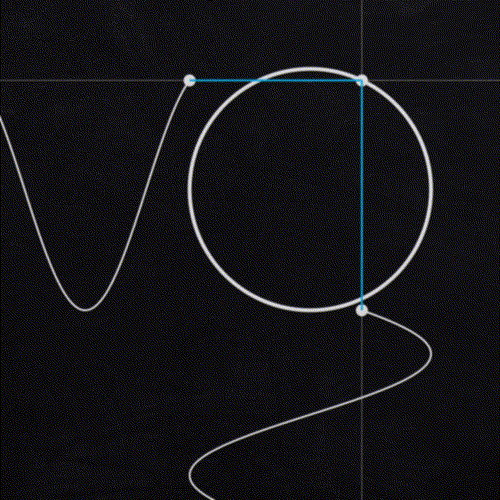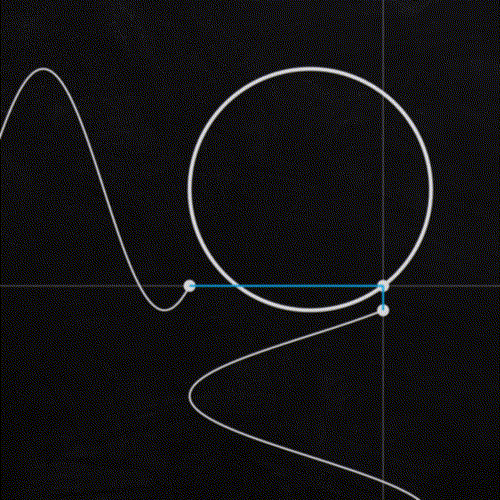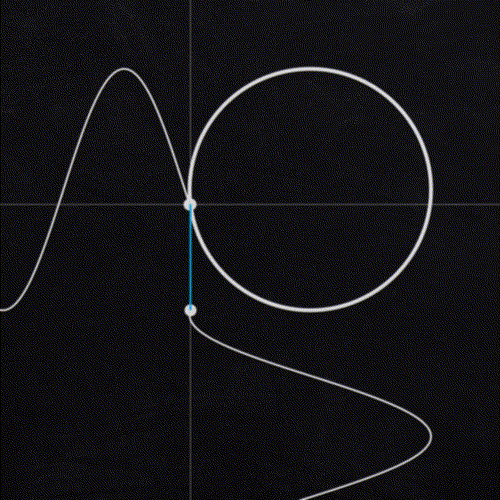
The looping noise technique comes down to the geometric relationship between sine and cosine waves. Both are periodic functions, meaning they return to the same value at regular intervals, meaning they naturally loop on their own. When I first attempted creating looping noise, my instinct was to use a sine shaped LFO (low frequency oscillator) to translate the z axis. The issue I encountered is that sine waves do not have constant velocity. As the curve changes direction, there is a point where velocity is 0. The result was motion that slows down, stops and reverses. It created a looping animation, but what if we want smooth motion throughout our loop?
The solution is to use a sine and cosine wave in tandem to drive the motion. As seen in the animation to the left, if we graph sine and cosine ( sin(x), cos(y) ) we get a unit circle. Notice how the dot moving around the circle travels at a constant speed, and makes a complete loop.
To utilize this relationship, we need to drive our noise motion using two parameters instead of one. This is where 4D noise comes in handy which gives us an extra dimension to translate our noise. Plugging a sine wave into translate z, and a cosine wave into the translate 4D will give us noise that animates continuously, and can easily be looped at different lengths.
Generating a circle with Sine and Cosine.
Étienne Jacob’s version in processing.
My recreation in TouchDesigner.